چرا بعضی افراد فکر میکنند ۵=۲+۲
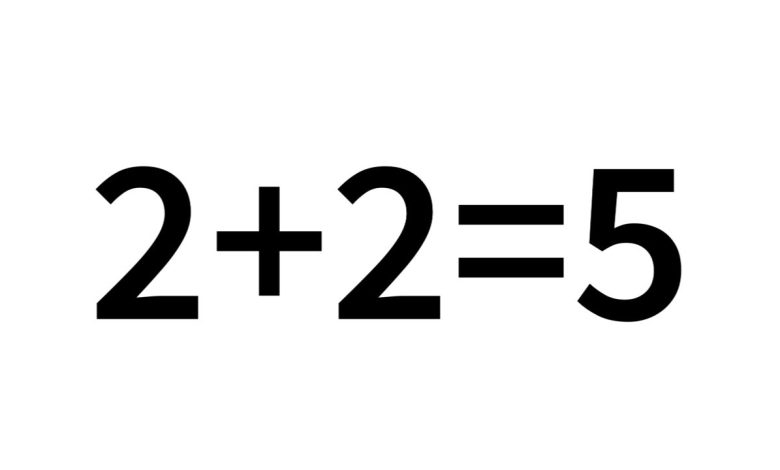
مسئلهای بهظاهر ساده مانند ۲+۲ زمانی به یک پارادوکس تبدیل شد که زمینههای دنیای واقعی وارد ماجرا شدند و همین امر، بحثهای کریم کار (Kareem Carr) درباره تعاریف و اصول موضوعه را برانگیخت. کریم کار نشان میدهد که چگونه زمینه میتواند حساب را دچار انحنا کند؛ برای نمونه، زاویهها که در مقدار ۲π رادیان به خود بازمیگردند یا گرد کردن که میتواند ۲.۳+۲.۳ را به ۵ تبدیل کند. این ایده به آمار و سیاست نیز گسترش مییابد و هشدار میدهد که امتیازهایی مانند IQ یا سنجیدن احساسات میتوانند گمراهکننده باشند.
روی کاغذ، این یکی از سادهترین مسائل ریاضی در جهان است. اگر در حال شمارش چیزی مانند پیچها در یک فروشگاه ابزار باشید، پاسخ کاملاً سرراست است. اما در زمینههای دیگر، مرزها محو میشوند. اگر ۰.۴۸ لیتر سرکه را با ۰.۴۸ لیتر جوششیرین ترکیب کنید و واکنش حاصل ۱.۲ لیتر مایع کفآلود تولید کند، آیا این به معنای آن است که ۲+۲ برابر با ۵ میشود؟
ما پیشفرضهایی را وارد جهان ریاضیات میکنیم. در این مورد، اعداد شمارشی ساده، یعنی اعداد صحیح ۱، ۲، ۳ و مانند آنها، شکافی را میان انتزاع ریاضی و کاربرد آن نشان میدهند. ریاضیدانان با استفاده از گزاره ۲+۲=۴ بهعنوان خوراک فکری، در حال بررسی شرایطی هستند که در آنها ۲+۲ عملاً برابر با ۴ نیست، دستکم نه به شکلی منظم. این تفسیرها را میتوان به پرسشهای بزرگتری در معرفتشناسی گسترش داد، یعنی اینکه چگونه آنچه را میدانیم، در حقیقت میدانیم!
چند سال پیش، کریم کار، دانشجوی دکترای آمار زیستی در دانشگاه هاروارد، بحثی با این عنوان که آیا ۲+۲ میتواند برابر با ۵ باشد را در شبکه اجتماعی X شعلهور کرد.
او در رشتهتوییت خود، تأکید کرد که اعداد شمارشی، انتزاعهایی از چیزهای واقعیِ زیربنایی در جهان هستند و به همین دلیل، باید مراقب باشیم که این انتزاعها هنگام ورود به سناریوهای دنیای واقعی چگونه حقیقت را دچار انحراف میکنند. حساب در کتاب درس بهخوبی کار میکند، اما در عمل اغلب با پرسشهای زمینهای مواجه میشود که اجزای یک کل، تقریبها یا بردارهای مرتبطتر را در نظر نمیگیرند.
برای مثال، اگر درجات کامل را به یک زاویه اضافه کنید، سرانجام به زاویهای میرسید که اندازه آن ۲π رادیان است. اما زاویهای با اندازه ۲π رادیان همان جهتگیری زاویهای با اندازه ۰ رادیان را دارد، بنابراین اینکه زاویه ۰ رادیان است یا ۲π رادیان به زمینه بستگی دارد. به همین قیاس، اگر بهجای چهار دور کامل، یک پیچ را پنج دور کامل بچرخانید، یعنی بهترتیب ۸π رادیان در برابر ۱۰π رادیان، جهتگیری پیچ یکسان میماند، اما در یکی از این حالتها پیچ عمیقتر در چوب فرو رفته است.
پاسخهایی که به توییت کریم کار داده شد، نمونههای دیگری از محدودیتهای حساب در دنیای واقعی را نشان میداد. بسیاری اشاره کردند که دو حیوان میتوانند از طریق تولیدمثل به سه تبدیل شوند یا حتی بسته به پارامترها به یک برسند، یا اینکه دو ماشین میتوانند با استفاده از قطعات یدکی هر کدام و کمی کار دستی به سه ماشین تبدیل شوند. دیگران یادآور شدند که عدد ۲.۳ به ۲ گرد میشود، اما ۲.۳+۲.۳ به ۵ گرد میشود، و از اینرو تحت یک فیلتر خاص میتوان به نتیجه ۲+۲=۵ رسید.
بهطور کلی، این تصور که ما بهطور ذاتی اعداد شمارشی، یعنی فقط مقادیر صحیح و نه کسرها یا اعشار، را میآموزیم، یک برداشت نادرست رایج در میان افرادی است که در ریاضیات یا رشد انسانی آموزش ندیدهاند. کودکان خردسال اعداد را یکییکی و از طریق شمارش میآموزند، اما تنها زمانی شروع به یادگیری شمارش پیشرفتهتر، یعنی اعداد بزرگتر، میکنند که بتوانند کمیتها را بهسرعت تشخیص دهند. برای مثال، زمانی شمارش تا ۷ برای ما آسانتر میشود که بتوانیم یک گروه چهارتایی را فوراً تشخیص دهیم و سپس پنجمین، ششمین و هفتمین مورد را بشماریم. شمارش، مهارتی آموختنی و غیرطبیعی است؛ حتی حیوانات غیرانسانی که میتوانند تا چهار یا پنج بشمارند، مانند سگها و شامپانزهها. بنابراین تحمیل اعداد شمارشی انتزاعی بر دنیای واقعی تنشی ذاتی ایجاد میکند.